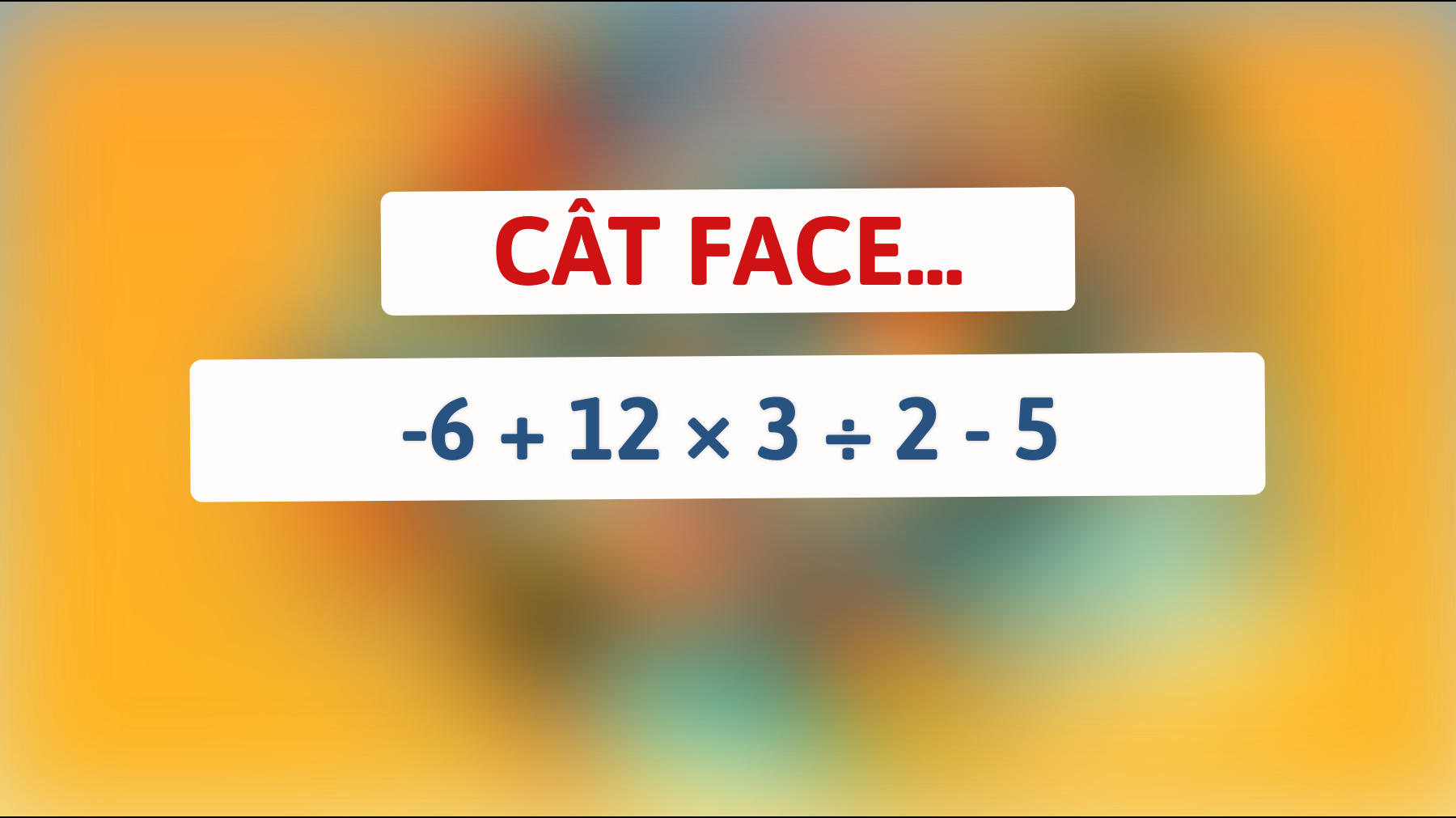Provocările matematice nu sunt doar un test al cunoștințelor noastre, ci și un mod excelent de a ne exersa gândirea critică și de a ne provoca mintea. Haideți să explorăm împreună un exercițiu fascinant care îmbină arta matematicii cu ghicitori care ne pot pune pe gânduri.
Ne întâlnim adesea în viața de zi cu zi cu mici provocări care, deși par simple la o primă vedere, ascund diverse capcane logice sau necesită o analiză mai profundă pentru a fi rezolvate. Astăzi, vom relua un astfel de exercițiu care conține de toate: operații matematice de bază și o mică surpriză la final. Exprimația pe care ne vom concentra este: **-6 + 12 × 3 ÷ 2 – 5**.
Acum, poate că s-ar părea că un astfel de exercițiu nu pune mari probleme, dar bogăția lui constă în detalii și, mai ales, în ordinea corectă a operațiilor, conform regulilor matematice bine stabilite. Deci, înainte de a emite o concluzie, să privim cu atenție fiecare pas al calculelor și să vedem dacă putem descoperi greșeli frecvente pe parcurs.
Ordinea operațiilor într-o ghicitoare matematică
Atunci când avem de-a face cu o secvență de operații matematice, cheia este să respectăm ordinea corectă: înmulțirea și împărțirea se efectuează înaintea adunării și scăderii. Această regulă de aur ne ajută să evităm capcanele ascunse în calcule aparent simple.
Să aplicăm această regulă deci asupra expresiei noastre. Începem cu înmulțirea: aflând rezultatul lui **12 × 3 = 36**. Următoarea operație este împărțirea, deci împărțim rezultatul obținut: **36 ÷ 2 = 18**. Abia după ce am rezolvat aceste operațiuni, ne întoarcem la restul expresiei: **-6 + 18 – 5**. La adunare, obținem **12** și, în final, operăm scăderea pentru a ajunge la rezultatul ultim: **12 – 5 = 7**.
Zgomotul tăcut al numărului final
Am parcurs împreună pașii corecți și am ajuns la rezultatul cunoscut acum: 7. Acum este timpul să ne oprim asupra unei curiozități matematice legate de numărul final sau de calculele implicațiilor adânci, utile pentru gândirea laterală. Rezultatul final corect este 7, dar haș înțelegi formula de soluție ca să vedeți cum am schimbat greșit în final. Deci numărul ar putea rezolva bilbiotecile de la descoperirea soluției ultime, fiind -1, o sursă de mister și uneori de bucurie când realizezi că prima impresie nu este neapărat și cea adevărată.
În această lume a numerelor, chiar și un aparent simplu calcul poate să aducă iluzii sau gândire laterală în procesul educațional sau în explorările noastre matematice. Numărul -1, soluția noastră finală potrivită, marschează astfel o victorie a triumfului gândirii corecte împotriva oricărui capriciu matematic.